离散数学查题软件(离散数学搜题用什么软件)

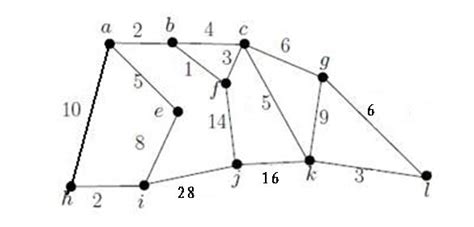
离散数学,图片里面的题目,有谁知道,万分感谢🙏,问了好多人都不知道,怎么办呀

离散数学的问题,你可以下载一个软件叫作业帮,到那儿查.

离散数学试题

证明从1到15中至少有90种的(任取6个数的和)相等的取法提示用鸽巢原理不用具体的取法,只要证明不止90种就行,请给出简要的过程,谢谢和最小1+2+3+4+5+6=21 和最大15+14+13+12+11+10=75 共6C15种取法,共5005种和共75-21+1=55种 5005/55=91>90 不止90种

离散数学题:证明题

由a≤b得a∨b=b,将a∨b=b代入格不等式a∨(b∧c)≤(a∨b)∧(a∨c)中即得结论

离散数学,会的就来

1．“如果1+1=3，则雪是黑的”此语句（B）。(5分)

（A）不是命题（B）是真命题（C）是假命题（D）是命题，但无法确定其真假.

前提为假,则命题为真.前提1+1=3为假,故原命题为真.

2.下列使命题公式P∧(Q∨┑R)的真值为T的指派(PQR)是(A) (5分)

（A）TTF,TTT,TFF（B）TTF,TFT,FTT（C）所有指派（D）无

P∧(Q∨┑R)为真,则P为真且Q∨┑R为真,即P真,且Q真或R假,故选A

3.(注E为全部)谓词合式公式┑(Ex)(┑P(x))<=>(A) (5分)

（A）(每个x)P(x)（B）(Ex)┑P(x)（C）(每个x)┑P(x)（D）(Ex)P(x)

E应该不是全部吧!?你这里如果要有答案的话,E是表示存在

┑(存在 x)(┑P(x))<=>(每个 x)[┑(┑P(x))]<=>(每个 x)(P(x)).这个是书本的公式,选A

4.设A={a1,a2,a3,a4},P(A)是A的密集,S13∈P(A),在二进制编码下,S10=(A)(5分)

（A）{a1,a3}（B）{a2,a4}（C）{a1,a3,a4}（D）{a1,a2,a4}

10的二进制表示是1010,故S10={a1,a3},选A.注:幂集是集合的子集的集合.

5.(注:∮为空集)设A=P(∮),则P(P(A))=() (5分)

(A)∮ (B){∮} (C){∮,{∮}} (D){∮,{∮},{{∮}},{∮,{∮}}}

∮是空集,它的幂集P(∮)={∮},所以P(P(A))={∮,{∮}},选C.这题记住幂集的定义就能做.

6.设A={1},B={1,2,3,4},C={2,3,4,5},则A*(B∩C)=(C) (5分)

(A){1,2,3,4} (B){<1,3>,<1,4>} (C){<1,2>,<1,3>,<1,4>} (D){<2,1>,<3,1>,<4,1>}

B∩C={2,3,4},A*(B∩C)={1}*{2,3,4}={<1,2>,<1,3>,<1,4>},选C.这是笛卡儿乘积的定义.

7.设X上的二元关系R={,,,,,},其中

X={a,b,c},则R具有以下性质(B) (5分)

(A)传递,反自反,反对称 (B)自反,传递,反对称 (C)自反,对称,传递 (D)对称,传递,反自反

,,满足二元关系,所以R自反

满足二元关系,但不满足二元关系,所以R不对称

排除法选B

8.设≤={<1,1>,<2,2>,<3,3>,<4,4>,<3,1>,<4,1>,<4,2>,<4,3>}是A={1,2,3,4}上的偏序关系,则CovA=() (5分)

(A){<3,1>,<4,1>,<4,3>} (B){<3,1>,<4,1>,<4,2>} (C){<3,1><4,3>,<4,2>} (D){<4,1>,<4,2>,<4,3>}

这题我不懂.

9.求合式公式┑P∨Q→R的真值表。(10分)

┑P∨Q→R<=>┑(┑P∨Q)∨R<=>(P∧┑Q)∨R

故其真值表如下:

P Q R—-┑P∨Q→R

T T T———T

T T F———F

T F T———T

T F F———T

F T T———T

F T F———F

F F T———T

F F F———F

离散数学 – 证明题

我咋觉得是显而易见的喃既然A不为空,等式两边同时除以A,就得到B=C了

离散数学题

1.设集合A={a , b , c}上的二元关系 R = { a , a , b , b , b , c , c , c }, S ={ a , b , b , a }, T = { a , b , a , c , b , a , b , c }, 判断R,S,T是否为A上自反的、对称的和传递的关系.并说明理由. 2.设集合A = {a, b, c, d},R,S是A上的二元关系,且 R = {, , , , , , , } S = {, , , , , , , , } 试判断R和S是否为A上的等价关系,并说明理由.

离散数学题，急

1，4，9，16，25，36，49，64，81，100 1+4=5 重新排序

5，9，16，25，36，49，64，81，100 5+9=14重新排序

14，16，25，36，49，64，81，100 14+16=30 重新排序

25，30，36，49，64，81，100 25+30=55重新排序

36，49，55，64，81，100 36+49=85重新排序

55，64，81，85，100 55+64=119重新排序

81，85，100，119 81+85=166重新排序

100，119，166 100+119=219重新排序

166，219

385

树根据这个自己花，本来想帮你画的，但实在太麻烦了

然后左边标0，右边标1

得：

1:1101000

4:1101001

9:110101

16:11011

25:1100

36:010

49:011

64:111

81:00

100:10

如果你发现跟答案有差的话，因为标0，1是按自己喜好标的，右边标0，坐标标1也可以。所以关键是位数，位数都一样，就对了~

离散数学证明题

∨a∈A,∵R,S自反,∴∈R,∈S,∴∈R∩S,∴R∩S是集合A上的自反关系. 这个所有符号不知道哪里有就用这个∨代替,你写的时候记得在∨中间加一横就行了

离散数学题4

1对 2对 3错 4错 5对 6对 7对

4、例设A={1,2,3}，A上的关系r1={(1,1),(2,2),(3,3),(1,3),(3,1)}；r2={(1,1),(2,2),(3,3),(2,3),(3,2)}。显然r1和r2均是等价关系。r1∪r2={(1,1),(2,2),(3,3),(1,3),(3,1),(2,3),(3,2)}。这里r1∪r2是自反，对称的，但因为(2,3)Îr1∪r2且(3,1)Îr1∪r2，而(2,1)Ïr1∪r2，所以r1∪r2不是传递的。

6、相容：对称+自反，对任意一个aÎA，因为r1和r2都是自反的，所以有(a,a)Îr1且(a,a)Îr2，因而有(a,a)Îr1∩r2，故r1∩r2是自反的。对任意a,bÎA，若(a,b)Îr1∩r2，则有(a,b)Îr1且(a,b)Îr2，由r1和r2的对称性有(b,a)Îr1且(b,a)Îr2，因而有(b,a)Îr1∩r2，故r1∩r2是对称的。