排课软件的业务处理流程,排课管理软件提高一对一排课效率

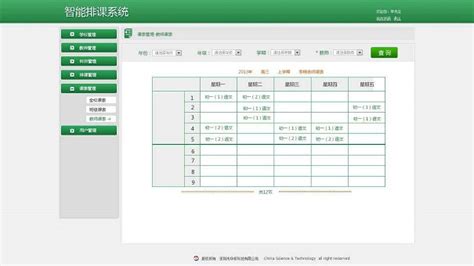
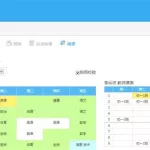
学校管理系统都是怎么进行排课的?

不同的管理系统,排课的方式不同的,但是目的都是一样的抄,就是帮助学袭校完成课程安排,可能有的系统的排课操作比较复杂,所以还是要选择一些排课操作便捷的2113管理系统,才能真正提升排课管理效率,就比如学来蜂管理系统,它5261对于课程安排的功能设计是非常智能的,并且操作方式十分便捷,同时4102系统提供的预防以及检测机制,能更好的降低排课冲突的概率1653,所以还是值得使用的

培训机构的排课软件用的什么样的.

培训机构排课的最大目的是将教师和教室的资源最大化,但是一旦课程多了,可能人工排课就会顾此失彼,想排好工作量就会非常大.从需求场景出发,可以以下集中排课主线: 1、课程为主:将课程放在合适的日期中排课,比较简单,但实际应用不多; 2、班级为主:根据班级同学的需求定一个开课日期,需要考虑学院报名时的需求; 3、教师为主:根据教师空闲时间段排课,和以上1、2结合排课,比较复杂; 4、教室为主:根据教室空闲时间段排课,和以上1、2、3条件结合排课,非常复杂; 综上,以上几个维度排课基本可以解决实际排课中90%的需求,您可以免费试用一下课栈互联系统看看能不能满足需求.

百策早教管理软件的简述

百策早教中心管理软件（原MicroCrm早教管理系统、易迈通早教管理系统）是针对早教机构管理者使用的一款强大管理系统，功能强大，操作便捷，实属国内第一款真正意义上的早教中心管理软件。

版本：单店版（适合只有一家早教机构使用）多店版（适合多家早教机构使用）

一、系统概要

百策早教管理系统是根据国内早教行业管理特点和国外成熟的管理理念，参考近百家早教中心的实际需求和使用习惯，开发出符合国内早教行业的早教管理系统。本系统集员工管理、绩效统计、活动管理、客户关系管理、事件管理、事件提醒、班级排课管理、学员上课管理、IC刷卡上课、合约管理、财务管理、报表统计等管理为一体的综合信息化管理系统。通过本系统能有效提升早教机构的工作效率与工作质量，协助早教机构开拓、管理业务，是早教机构运营、管理的得力助手。

早教管理系统为独立开发，拥有自主的知识产权，因此凭靠专业的技术能满足广大早教中心企业提出的各种特殊应用要求，同时我们也可以根据早教中心不同的需求提供定制开发服务。

二、软件特色

百策早教排课及管理系统主要面向国内加盟早教企业或自营早教企业，通过对早教中心活动、新客户添加、跟踪、试听预约、签约、排课、课评、顾问跟踪服务、续课等经营环节的信息全程记录、跟踪、传递和分析，规范企业业务处理流程，实现对中心招生情况、上课情况的动态监控和全方位管理，从而使整个中心的课程质量和服务质量有更好的提高。

整个早教管理系统（包括排课、课评、客户关系、客户服务跟踪）都是以“服务学员”为核心思想，按照系统管理员、中心主任（经理）、前台、老师、课程顾问等岗位而进行的功能版块设计，进而降低了企业的操作门槛和使用成本，使本系统能与企业更紧密、低成本的结合。

百策早教排课及管理系统所有版本均是采用C/S 三层，使系统数据层、业务逻辑层和前台出现层逻辑上完全独立，方便企业正常使用后的功能升级和系统部署，另外因采用三层结构，使数据层从系统中独立出来，可以在广域网上有更好的表现；

系统区别与市面上其他 B/S 模式管理软件（网页模式），百策早教管理系统的设计体系更注重与业务流程和业务事务处理方面（课时表、排课处理、刷卡上课、充值消费、积分等业务模块），以最低的成本使软件和企业相结合；另外系统的数据库默认为在企业内部，充分保障了企业数据的安全性。

培训学校排课软件

软件工程师还是很不错的,只不过那里的学费贵了点!如果想学的话,建议到沿海地区的深圳那里去看看,那里有个深圳华夏软件教育还是很不错的,不但学费要便宜一半多,而且课程也是一样的,师资力量也很不错的呢!网址:www.huaxiapx.cn

怎样做好高校排课？

1课题背景与研究意义

排课问题早在70年代就证明是一个NP完全问题，即算法的计算时间是呈指数增长的，这一论断确立了排课问题的理论深度。对于NP问题完全问题目前在数学上是没有一个通用的算法能够很好地解决。然而很多NP完全问题目具有很重要的实际意义，例如。大家熟悉地路由算法就是很典型的一个NP完全问题，路由要在从多的节点中找出最短路径完成信息的传递。既然都是NP完全问题，那么很多路由算法就可以运用到解决排课问题上，如Dijkstra算法、节点子树剪枝构造网络最短路径法等等。

目前大家对NP 完全问题研究的主要思想是如何降低其计算复杂度。即利用一个近似算法来代替，力争使得解决问题的时间从指数增长化简到多项式增长。结合到课表问题就是建立一个合适的现实简约模型，利用该简约模型能够大大降低算法的复杂度，便于程序实现，这是解决排课问题一个很多的思路。

在高等院校中，培养学生的主要途径是教学。在教学活动中，有一系列管理工作，其中，教学计划的实施是一个重要的教学环节。每学期管理人员都要整理教学计划，根据教学计划下达教学任务书，然后根据教学任务书编排课程表。在这些教学调度工作中，既有大量繁琐的数据整理工作，更有严谨思维的脑力劳动，还要填写大量的表格。因此工作非常繁重。

加之，随着教学改革的进行及“211”工程的实施，新的教育体制对课表的编排提出了更高的要求。手工排课时，信息的上通下达是极其麻烦的，而采用计算机排课，教学中的信息可以一目了然，对于优化学生的学习进程，评估每位教师对教学的贡献，领导合理决策等都具有重要的意义，必将会大大推进教学的良性循环。

2课题的应用领域

本课题的研究对开发高校排课系统有指导作用。

排课问题的核心为多维资源的冲突与抢占，对其研究对类似的问题（特别是与时间表有关的问题：如考试排考场问题、电影院排座问题、航空航线问题）也是个参考。

3 课题的现状

年代末，国外就有人开始研究课表编排问题。1962年，Gotlieb曾提出了一个课表问题的数学模型，并利用匈牙利算法解决了三维线性运输问题。次后，人们对课表问题的算法、解的存在性等问题做了很多深入探讨。但是大多数文献所用的数学模型都是Gotlieb的数学模型的简化或补充，而至今还没有一个可行的算法来解决课表问题。

近40年来，人们对课表问题的计算机解法做了许多尝试。其中，课表编排的整数规划模型将问题归结为求一组0-1变量的解，但是其计算量非常大。解决0-1线性优化问题的分支一定界技术却只适用也规模较小的课表编排，Mihoc和Balas（1965）将课表公式化为一个优化问题，Krawczk则提出一种线性编程的方法。Junginger将课表问题简化为三维运输问题，而Tripathy则把课表问题视作整数线性编程问题并提出了大学课表的数学模型。

此外，有些文献试图从图论的角度来求解排课表的问题，但是图的染色问题也是NP完全问题，只有在极为简单的情况下才可以将课表编排转化为二部图匹配问题，这样的数学模型与实际相差太远，所以对于大多数学校的课表编排问题来说没有实用价值。

进入九十年代以后，国外对课表问题的研究仍然十分活跃。比较有代表的有印度的Vastapur大学管理学院的ArabindaTripathy、加拿大Montreal大学的Jean Aubin和Jacques Ferland等。目前，解决课表方法的问题有：模拟手工排课法，图论方法，拉格朗日法，二次分配型法等多种方法。由于课表约束复杂，用数学方法进行描述时往往导致问题规模剧烈增大，这已经成为应用数学编程解决课表问题的巨大障碍。国外的研究表明，解决大规模课表编排问题单纯靠数学方法是行不通的，而利用运筹学中分层规划的思想将问题分解，将是一个有希望得到成功的办法。

在国内，对课表问题的研究开始于80年代初期、具有代表性的有：南京工学院的UTSS（A University Timetable Scheduling System）系统，清华大学的TISER（Timetable SchedulER）系统，大连理工大学的智能教学组织管理与课程调度等，这些系统大多数都是模拟手工排课过程，以“班”为单位，运用启发式函数来进行编排的。但是这些系统课表编排系统往往比较依赖于各个学校的教学体制，不宜进行大量推广。

从实际使用的情况来看，国内外研制开发的这些软件系统在实用性上仍不尽如人意。一方面原因是作为一个很复杂的系统，排课要想面面俱到是一件很困难的事；另一方面每个学校由于其各自的特殊性，自动排课软件很难普遍实用，特别是在调度的过程中一个很小的变动，要引起全部课程的大调整，这意味着全校课程大变动，在实际的应用中这是很难实现的事。

4解决NP问题的几种算法及其比较

解决NP完全问题只能依靠近似算法，所以下面介绍几种常用算法的设计思想，包括动态规划、贪心算法、回溯法等。

动态规划法是将求解的问题一层一层地分解成一级一级、规模逐步缩小的子问题，直到可以直接求出其解的子问题为止。分解成的所有子问题按层次关系构成一颗子问题树。树根是原问题。原问题的解依赖于子问题树中所有子问题的解。动态规划算法通常用于求一个问题在某种意义下的最优解。设计一个动态规划算法，通常可按以下几个步骤进行：

1. 分析最优解的性质，并刻划其结构特征。

2. 递归的定义最优解。

3. 以自底向上的方式计算出最优解。

4. 根据计算最优解时得到的信息，构造一个最优解。

步骤1~3是动态规划算法的基本步骤。在只需要求出最优解的情形，步骤4可以省去。若需要求出问题的一个最优解，则必须执行步骤4。此时，在步骤3中计算最优解时，通常需记录更多的信息，以便在步骤4中，根据所记录的信息，快速地构造出一个最优解。

（二）贪心算法

当一个问题具有最优子结构性质时，我们会想到用动态规划法去解它，但有时会有更简单、更有效的算法，即贪心算法。顾名思义，贪心算法总是做出在当前看来最好的选择。也就是说贪心算法并不是整体最优上加以考虑，他所作出的选择只是在某种意义上的局部最优的选择。虽然贪心算法不是对所有问题都能得到整体最优解，但对范围相当广的许多问题它能产生整体最优解，如图的算法中单源最短路径问题，最小支撑树问题等。在一些情况下，即使贪心算法不能得到整体最优解，但其最终结果却是最优解的很好的近似解。

在贪心算法中较为有名的算法是Dijkstra算法。它作为路由算法用来寻求两个节点间的最短路径。Dijkstra算法的思想是：假若G有n个顶点，于是我们总共需要求出n-1条最短路径，求解的方法是：初试，写出V0(始顶点)到各顶点(终顶点)的路径长度，或有路径，则令路径的长度为边上的权值；或无路经，则令为∞。再按长度的递增顺序生成每条最短路径。事实上生成最短路径的过程就是不断地在始顶点V何终顶点W间加入中间点的过程，因为在每生成了一条最短路径后，就有一个该路径的终顶点U，那么那些还未生成最短路径的路径就会由于经过U而比原来的路径短，于是就让它经过U。

（三）回溯法

回溯法有“通用的解题法”之称。用它可以求出问题的所有解或任一解。概括地说，回溯法是一个既带有系统性又带有跳跃性的搜索法。它在包含问题所有解的一颗状态空间树上，按照深度优先的策略，从根出发进行搜索。搜索每到达状态空间树的一个节点，总是先判断以该节点为根的子树是否肯定不包含问题的解。如果肯定不包含，则跳过对该子树的系统搜索，一层一层地向它的祖先节点继续搜索，直到遇到一个还有未被搜索过的儿子的节点，才转向该节点的一个未曾搜索过的儿子节点继续搜索；否则，进入子树，继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时，要回溯到根，且根的所有儿子都已被搜索过才结束；而在用来求问题的任一解时，只要搜索到问题的一个解就可结束。

加油！

c++排课系统的算法

这个不是排列组合题目吧？如果不是，那就很简单。大致说下思路，自己实现吧。

把学校机房的课时按每小时或者按几个小时为单位编成一个数据结构。这个具体看学校怎么安排上机课，如果最小单位为2小时，当然以2小时为单位，如果有班级只上半小时的上机课当然以半小时为单位。比如一周5天每天10小时我们可以把它编成50个单位的一个数据结构。可以为数组，可以为链表，当然也可以为更复杂的结构，看你的需要。简单的机房上机课时结构基本子元素为：起止时间、已安排班级（若未安排则为空）、已安排老师

把班级和老师也储存在一个数据结构里。然后确定班级排上机课的原则。比如是平均分配机时，那么将每个班级增加一个计数器。那么班级的数据结构每个元素至少要有这么几个子元素：班级标识、班级计数器、班级空闲时间表。排上机课的时候，首先取出机房上机课时的数据结构，取出第一个元素，然后遍历存储班级信息的数据结构，优先取出班级计数器最小的班级，查看这个班级这时是否有课，无课则插入到上机课时的数据结构中，同时将班级计数器加一，有课则选择下一个计数器数字最小的元素。（计数器只是表示班级安排了多少上机课，也可以用一个数字代替，仅仅表示权重，比如计算机系的班级权重就可以调高。建议将整个链表中计数器数字的最小值保存在这个链表的某处，使得访问者一开始就能得到而不用访问所有元素）。重复上述过程，直到所有上机课时都被分配。

老师的分配过程和上述班级分配类似。

看来是新手，加油！