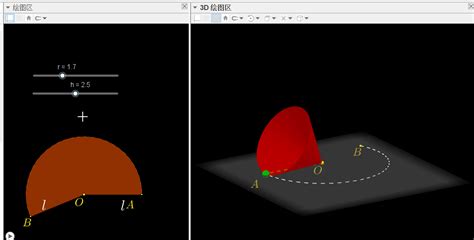
初中数学动点问题如何来做成动态的动画?
如果是ppt,可以用一个图形掩盖,然后让这个图形以“擦除”的方式消失,便有了动点的感觉
数学动点~!~高手速度.
精简版 1:BO=4 2:因为BM:MO=1:2,所以DB=0A/2=1,D的坐标是(1,2根3),OD:Y=2根3 X 3:根据t可以得P得坐标,再根据A的坐标可以得到AP的函数,与OD的函数联立可以解出E的坐标,其纵坐标为三角形OAE的高,其底边是2,所以面积可以得,()另外还一种情况是P在B和M之间,这就有点麻烦,就不多解释,呵呵
急!!!!几何数学动点
题目都不清楚好像。。 E,F都是从哪里开始运动的 到哪里停止?
我的分析是E从B,F从C。。
解:当0≤t≤4时。。
S△AEF=48-3个直角三角形,会吧?
当4<t≤6时,一个样子
至于到哪里停止没说明,不过都给你分成这样了,你也会了吧!。。。
数学动点与函数
解:(1)
在Rt△HCO中,由于∠OCH=60°,∠OCH的对边为2√3,
所以CB= (2√3)/sin60°=4,OC=2+2=4
所以:OH=∠OCH的对边=2√3
(2)
根据题意得:OQ=t,HP=t。
所以OP=OH-PH=(2√3)-t
所以:三角形OPQ的面积S=(1/2)*OQ*sin60°*OP
即:S=t(1/2)[(√3)/2][(2√3)-t]
S=[(-√3)/4]t^2+(3/2)t
由于-√3<0,所以S=[(-√3)/4]t^2+(3/2)t有最大值,
当t=-(3/2)/{2[(-√3)/4]}=√3时,S值最大为:(√3)/4
即:S与 t之间的函数关系式为S=[(-√3)/4]t^2+(3/2)t ,t为 t为值时√3时,三角形OPQ的面积最大,最大值是(3√3)/4
(3)
第一种情况:
过B点作BD垂直OC交直线OH于一点,过这点作OC的平行线,交OB于M点,交OA于Q点,交CB于N点。那么BD、OH的交点就是P点。△MOP是等腰三角形
(证明思路是:QP平行OD,OH平分角BOC,可得△MOP是等腰三角形。另外:PH=PD=OQ=t)
由P点是等边三角形OCB的重心得:HP=(1/3)OH=(2√3)*(1/3)=(2√3)/3
即:t=(2√3)/3
此时三角形OPQ的面积S=[(-√3)/4]t^2+(3/2)t
={[(-√3)/4]t^2+(3/2)}*[(2√3)/3]=(2/3)√3
第二种情况:
作∠OBD的平分线交OH于P点,链接DP并延长交于BO于M点,交AO于Q点,则OM=OP
三角形MOP也是等腰三角形。P点是三角形ODB的内心。
可证明△BHP和△DOQ是全等的等腰直角三角形,从而有HP=OQ=t=2
可证明△OPD和△OMQ全等,从而有OM=OP
将t=2带入S=[(-√3)/4]t^2+(3/2)t中得:S=3-√3
我想就这两种情况了,使MP=PO是不存在的,因为此时OA与MP平行了。
至于OM的值:当点Q和点P分别在线段OA和线段OH的中点时,OM的值最大,最大值是3/2
初三数学动点讲解
这个问题太宽泛了…动点可以跟函数结合,可以跟坐标系结合,可以出几何题.动点一般几何题是找特殊点,譬如“当XX满足什么关系时,使XX=XX”“当XX满足什么关系时,使XX+XX最短”,常记一些特殊点,譬如“修水坝”问题,会做会证.函数则是找关系,’求出X与XX的关系”,这时求出后注意写取值范围.坐标系则是与几何题类似
初二数学动点
K=1 时,为平行四边形 K=2 时,为直角梯形(很好证明) K=3 时,为等腰直角体形 设AD为2a DE=a 到这里都没错… 然后你设 BP为2a就不对了.. 这里P是动点..你怎么知道是2a..? 只能设BC为3a 然后按相似比K讨论.
初三数学动点
AD=5cm 直角三角形计算边长 AE=5/4x DE=5-5/4x DQ=2-1.25x 高h=PC=4-x S=1/2(2-1.25x)(4-x) 0 易知△ABC和△BCD共圆,圆心为BC中点.再根据圆周角知识可知,当AP平分∠BAC时,AP将过D点. 则有∠BDP=∠BCA=60°. 在△BPD中,作PE⊥BD于E,设ED=x,易知PD=2x,PE=BE=根3倍x 由BD=2倍根2=根3倍x+x,解得x=根6-根2.则PD=2倍(根6-根2) 点E怎么来的?你检查一下,有问题. 由题意,BC=4,∴T≤4,且A(10,0),B(7,4)P(2T,0),Q(7-T,4)E(4-T,0). QE=5 (1)PE=QE=5即2T-(4-T)=5即T=3 (2)PE=PQ即2T-(4-T)=根号(4²+(3T-7)²)即T=49/18 (3)QE=QP即T=2或T=4/3数学 三角形 动点
动点数学求高人