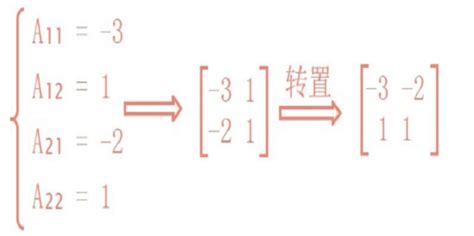
有没有功能强大的矩阵计算器软件,除了简单的加减乘除运算,还可以求逆矩阵、矩阵特征值、特征向量等等
有啊!功能强大的MATLAB软件!在网上可以下载到,安装到电脑里就可以完成除了简单的加减乘除运算,还可以求逆矩阵、矩阵特征值、特征向量等等.
介绍矩阵转置,求逆,相乘,求行列式值的运算工具
可以用matlab、mathematica、mathcad、zzllrr mather等等 excel也支持部分矩阵运算(用公式).
如何用卡西欧fx-991cnx计算矩阵,以及怎么计算逆矩阵
1.设置矩阵变量
进入矩阵模式后,选择1(MatA),根据需求设置矩阵的行与列。同理可设置MatB、MatC、MatD三个矩阵。
2.指定并编辑矩阵的变量数据
1)按OPTN+1(定义矩阵),然后在显示的菜单中,选择要向其指定数据的矩阵变量。
2)在出现的对话框上,使用一个数字按钮指定行数。
3)在出现的下一个对话框上,使用一个数字按钮指定行数。
4)使用显示的矩阵编辑器输入矩阵的元素。
3.编辑矩阵变量的元素
1)按OPTN+2(编辑矩阵),然后在显示的菜单中,选择要编辑的矩阵变量。
2)使用显示的矩阵编辑器编辑矩阵的元素。
4.矩阵答案存储
无论何时,只要在矩阵模式中执行的计算结果为矩阵,MatAns屏幕都将显示该结果。该结果还会指定给名为“MatAns”的变量。
参考资料来源:卡西欧官网-计算器fx-cnx说明书
怎么在EXCEL做矩阵求逆计算
Excel提供求逆矩阵的函数:MINVERSE,可以直接求一个方阵的逆.但要注意的是,求逆矩阵只能用数组公式,如已知的方阵在A1:C3——3*3的方阵,要在D1:F3中求其逆矩阵: 先选择D1:F3,即选择与已知方阵同样大小的空方阵区域,再输入公式: =MINVERSE(A1:C3) 同时按Ctrl+Shift+Enter三键输入数组公式,得到结果.
求3*3矩阵反数的算法,我也不知道是不是叫这名,inverse 直译是这个从美国学的,老师说用计算器
假设原矩阵是A,单位阵是E就是对角线上是1其余全为0的矩阵,构造的新的矩阵是(A,E)的时候,(可看为分块矩阵,就是两个矩阵直接拼了起来)只进行初等行变换变为(E,B)则B就是他的逆.(A,E)看成是一个3行6列的矩阵,进行行变换,前面怎么变,后面就是怎么变,例如说第一行加上第二行,就是第一行的六个元素分别加上第二行的六个元素.但是是以将前面3行3列化为单位阵为目的进行变换.
用初等矩阵求逆矩阵……
方法一、在原矩阵右边写出一单位矩阵,再利用行初等变换把原矩阵化成单位矩阵,先前写出的单位矩阵变化为原矩阵的逆. 方法二、在原矩阵的下边写出一单位矩阵,再利用列初等变换把原矩阵化成单位矩阵,…… 方法三、利用教材给出的公式(矩阵行列式的的倒数乘以伴随矩阵)
matlab算矩阵的逆的程序
matalb 有计算逆矩阵的函数 inv() 例如: >> A=magic(3) A = 8 1 6 3 5 7 4 9 2 >> inv(A) ans = 0.1472 -0.1444 0.0639 -0.0611 0.0222 0.1056 -0.0194 0.1889 -0.1028
线性代数 分块矩阵的逆矩阵计算
题:
求分块矩阵P=
A OC B
的逆矩阵。
其中A和B分别为n阶和m阶可逆矩阵。
解一:
设所求=
X Y
Z W
则积=
AX,AY;
CX+BZ,CY+BW
易见X=A逆,Y=0E,W=B逆,
C*(A逆)+BZ=0E,Z=-B逆*C*A逆。
即所求=
A逆,0E;
-B逆*C*A逆,B逆
解二:
求分块矩阵P=
A OC B
的逆矩阵。
其中A和B分别为n阶和m阶可逆矩阵。
令R=
A O
O B
S=
O O
C O
注意到S^2=O,…
计算逆矩阵
矩阵的逆等于伴随矩阵除以矩阵的行列式,所以现在只要求原矩阵的行列式即可。 A^*=A^(-1)|A|, 两边同时取行列式得 |A^*|=|A|^2 (因为是三阶矩阵)又|A^*|=4,|A|>0,所以|A|=2 所以A^(-1)=A^(*)/2,就是伴随矩阵除以2。特殊求法:(1)当矩阵是大于等于二阶时 :主对角元素是将原矩阵该元素所在行列去掉再求行列式,非主对角元素是原矩阵该元素的共轭位置的元素去掉所在行列求行列式乘以 , x,y为该元素的共轭位置的元素的行和列的序号,序号从1开始。主对角元素实际上是非主对角元素的特殊情况,因为x=y,所以 ,一直是正数,没必要考虑主对角元素的符号问题。(2)当矩阵的阶数等于一阶时,伴随矩阵为一阶单位方阵。(3)二阶矩阵的求法口诀:主对角线元素互换,副对角线元素加负号。 扩展资料:若|A|≠0,则矩阵A可逆,且其中,A*为矩阵A的伴随矩阵。证明:必要性:当矩阵A可逆,则有AA-1=I 。(其中I是单位矩阵)两边取行列式,det(AA-1)=det(I)=1。由行列式的性质:det(AA-1)=det(A)det(A-1)=1 则det(A)≠0,(若等于0则上式等于0)充分性:有伴随矩阵的定理,有 (其中 是的伴随矩阵。)当det(A)≠0,等式同除以det(A),变成 比较逆矩阵的定义式,可知逆矩阵存在且逆矩阵