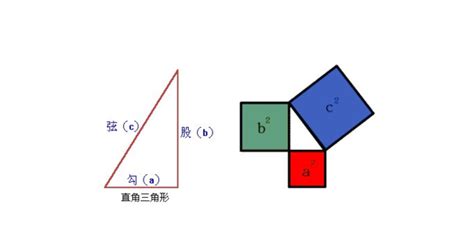
大家都知道3.4.5;5,12,13;8,15,17等都是勾股数组
这个观点是正确的
假设三个数都是奇数
奇数的平方也就是奇数乘以奇数,仍然是奇数
那么根据勾股定理
出现了奇数=奇数+奇数的情况
这与事实相悖,
所以原假设错误,
必有一个是偶数。
勾股数因为是满足直角三角形的数,所以也满足三角形的规律
那就是三个数中任意两个数相加都大于第三个数
任意两个数相减都小于第三个数
再一个就是
平方数的尾数只有可能为0、1、4、5、6、9
而这6个数中只有
0+1出现1
0+4出现4
0+5出现5
0+6出现6
0+9出现9
1+4出现5
1+9出现0
4+5出现9
4+6出现0
分析上面的情况可以看出,所有的情况中都含有0或5,而0或5只有尾数为0或5的数平方后才可能出现。
同时尾数为0的数和尾数为5的数都是5的倍数。
这样我们推断出一个规律:
勾股数中至少有一个数是5的倍数!
天啊,我真应该去学数学,我自己都觉得自己太猛了!!!
初二上学期数学所有知识点归纳
第十六章 分式
一、定义:如果A、B表示两个整式,并且B中含有字母,那么式子 叫做分式。
二、分式基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。
三、分式计算:分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
分式除法法则:分式除以分式,把除式的分子、分母颠倒置后,与被除式相乘。
分式乘方:分式乘方要把分子、分母分别乘方。
四、整数指数幂:(1) (2)较小数的科学记数法;
五、分式方程检验方法:将整式方程的解带入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解。(这个解是增根,原方程无解)。
第十七章 反比例函数
一、形如y= (k为常数,k≠0)的函数称为反比例函数;
二、反比例函数的图像属于双曲线;
三、性质:当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小;
当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大。
第十八章 勾股定理
一、勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么
二、勾股定理逆定理:如果三角形三边长a,b,c满足 ,那么这个三角形是直角三角形。
三、经过证明被确认正确的命题叫做定理。
四、我们把题设、结论正好相反的两个命题叫做互逆命题。如果把其中一个叫做原命题,那么另一个叫做它的逆命题。(例:勾股定理与勾股定理逆定理)
第十九章 四边形
一、平行四边形:
1、定义:有两组对边分别平行的四边形叫做平行四边形。
2、性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分。
3、判定:(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形;
(4)一组对边平行且相等的四边形是平行四边形。
(5)有两组对边分别平行的四边形叫做平行四边形。(定义)
4、三角形的中位线平行于三角形的第三边,且等于第三边的一半。
二、矩形:
1、定义:有一个角是直角的平行四边形叫做矩形。
2、性质:矩形的四个角都是直角;矩形的对角线平分且相等。
3、判定:(1)有一个角是直角的平行四边形叫做矩形。(定义)
(2)对角线相等的平行四边形是矩形。
(3)有三个角是直角的四边形是矩形。
4、直角三角形斜边上的中线等于斜边的一半。
三、菱形:
1、定义:一组邻边相等的平行四边形是菱形
2、性质:菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
3、判定:(1)一组邻边相等的平行四边形是菱形。(定义)
(2)对角线互相垂直的平行四边形是菱形。
(3)四条边相等的四边形是菱形。
4、S菱形=底×高 S菱形= ab(a、b为两条对角线)
四、正方形:
1、定义:有一组邻边相等的矩形是正方形。或有一个角是直角的菱形是正方形。
2、性质:四条边都相等,四个角都是直角;正方形既是矩形,又是菱形。
3、判定:(1)邻边相等的矩形是正方形。
(2)有一个角是直角的菱形是正方形。
五、梯形:
1、定义:一组对边平行,另一组对边不平行的四边形叫做梯形。
2、等腰梯形定义:两腰相等的梯形叫做等腰梯形。
性质:等腰梯形同一底边上的两个角相等;等腰梯形的两条对角线相等。
判定:同一底上两个角相等的梯形是等腰梯形;对角线相等的梯形是等腰梯形。
3、梯形的中位线分别平行于上、下两底,且等于上、下两底和的一半。
六、重心:
1、线段的重心就是线段的中点。
2、平行四边形的重心是它的两条对角线的交点。
3、三角形的三条中线交于疑点,这一点就是三角形的重心。
七、数学活动(教材115页):
1、折纸多60°、30°、15°的角证明方法(重点30°角)
2、宽和长的比是 (约为0.618)的矩形叫做黄金矩形。
第二十章 数据的分析
一、加权平均数:计算公式(教材125页。)
二、中位数:将一组数据按照由小到大(大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
三、众数:一组数据中出现次数最多的数据就是这组数据的众数(mode)。
四、极差:一组数据中的最大数据与最小数据的差叫做这组数据的极差(range)。
五、方差:
1、计算公式: ( 表示 的平均数)
2、性质:方差越大,数据的波动越大;方差越小,数据的波动越小,就越稳定。
六、数据的收集与整理的步骤:
1.收集数据 2.整理数据 3.描述数据 4.分析数据 5.撰写调查报告
求勾股数组大全
1.(3.4、5)2.(6、8、10)3.(5.12,13)4.(8、15.17)5. (2,24,25)6, (9,40, 41)7. (10, 24, 26)8. (11,60,61)9. (12、35, 37)10, (48, 55, 73)11. (12,16, 20)12. (13,84, 85)4. (20, 99, 101)13. (20, 21,29)15. (60,91,109)16. (15, 112、113)18.(19, 180, 181)17. (17, 144, 145)
勾股定理数字有无规律
如果三个正整数a、b、c,满足a2+b2=c2,那么这三个数就称为一组勾股数。据说,在公元前1000多年,我国古代数学家商高就发现了3,4,5 满足这一关系。更奇怪的是,古巴比伦人在更早的时候就列出了很多满足这个关系的数据组。古往今来,勾股数组被太多的人津津乐道,可见其神秘性和趣味性。
我在课后给学生布置了这样一个题目,请列出一些常见的勾股数组,仔细观察,看每组数之间有什么联系和规律?
因为曾经给学生介绍过关于勾股定理的证明的一些故事,关于定理的命名——“勾股定理”、“毕达哥拉斯定理”之争,关于《勾股方圆图注》、《青朱出入图》,美国总统对定理的证明以及画家达芬奇对这个定理的研究等,所以当这个课题提出以后,学生的兴趣分外浓厚。现在将他们发现的规律整理出来,供大家欣赏:
1、 勾股数中的三个数不能全是奇数。
2、 勾股数里的三个数要么全是偶数,要么只有一个偶数(即不可能出现只有两个偶数的情况)。奇数的平方为奇数,偶数的平方为偶数,而奇数+奇数=偶数 ,因此当两条直角边都为奇数时,斜边为偶数;当两条直角边都为偶数时,斜边为偶数;当两条直角边为一奇一偶时,斜边为奇数。
3、 大于2的任何一个整数都可以作为直角三角形的一条边长 ,而且可以很快地得到包含这个数在内的一组勾股数。 比如,给出一条直角边长为9 ,那么将9平方得81,然后将81分成相邻的两个正整数40 、41的和,就得到一组勾股数9,40,41。如果给出的一个数是偶数,也很简单,比如给出一个数12,那么12除以2得6,62-1=35,62+1=37,这样就得到勾股数12,35,37 。
4、 规律3可以用字母表示为:当n是奇数时,n, , 是一组勾股数。当n是偶数时,n, , 是一组勾股数。
5、 将规律4逆用,可以得到:(1)如果一组勾股数中两个较大的数相差1,那么这两个数的和就是第三个数的平方;(2)如果两个较大的数相差2,那么这个两个数中间所夹的整数是第三个数的一半的平方。比如:7,24,25 是一组勾股数,其中24+25 =72;8,15,17是一组勾股数,15、17中间所夹的整数16 恰是8的一半4的平方。证明起来也很简单。(1)的证明如下:设a,b,b+1 是一组勾股数,那么a2 +b2 =(b+1)2=b2+2b+1,于是得到a2=2b+1=b+(b+1) 即b+(b+1)=a2。(2)的证明与(1)类似。
6、 m2-1,2m,m2+1(m )是一组勾股数。
2n+1,2n(n+1),2n(n+1)+1 (n 是正整数)是一组勾股数。(当然,这应该算是毕达哥拉斯学派首先发现的)
这两组勾股数都可以通过勾股定理的基本公式得到证明。
7、6中的两个公式不能涵盖所有的勾股数,要想涵盖所有的勾股数,需要用m2-n2,2mn,m2+n2(m>n且、是正整数)。
如图1,四边形ABHC,ADEF都是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.(1)当正方形ADEF
(1)BD=CF成立,
理由是:∵四边形ABHC和四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∴∠BAC-∠DAC=∠DAF-∠DAC,
∴∠BAD=∠CAF,
在△DAB和△FAC中
AB=AC
∠DAB=∠FAC
AD=AF
∴△DAB≌△FAC(SAS),
∴BD=CF.
(2)①证明:∵△DAB≌△FAC,
∴∠FCA=∠DBA,
∵∠CMG=∠BMA,∠CAB=90°,
∴∠CMG+∠FCA=∠DBA+∠BMA=180°-∠CAB=90°,
∴在△CGM中,∠CGM=180°-90°=90°,
∴BD⊥CF.
②解:过点F作FN⊥AC于点N,
∵在正方形ADEF中,AD=
2 =AF,∠DAB=45°,
∴∠DAC=45°,∠FAN=45°,
∵FN⊥AC,
∴∠FNA=90°,
∴∠NFA=45°=∠FAN,
∴FN=AN,
∵四边形ADEF是正方形,
∴AD=AF=EF=
2 ,∠EFA=90°,
∴由勾股定理得:AE=2,
∴FN=AN=1,
连接BC,在等腰直角三角形ABC中,AB=AC=4,
则CN=4-1=3,BC=
AC2+AB2 =4
2 ,
即在Rt△FCN中,tan∠FCN=
FN
CN =
1
3 ,
在Rt△ABM中,tan∠ABM=tan∠FCN=
1
3 ,
∴AM=
1
3 AB=
本回答由提问者推荐
答案纠错|评论
奈子222
采纳率:65%擅长:暂未定制
为您推荐:
其他类似问题
2015-02-04
如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=A…
2015-02-07
(2014?江西样卷)如图,在△ABC中,点D、E分别是边A…
15
2016-03-15
初三几何题,求正解,要详细过程~
1
2013-11-17
1.如图,点E,F分别在线段AB,AC上,且AB⊥CE,AC…
1
2013-07-09
关于初中数学的题目
4
更多相关3,已知:四边形ABEF和四边形ACHD均为正方形,证明:(1)BD=CF (2)BD⊥CF的问题 >
正方形的相关知识
2011-04-14
正方形的体积怎么算?
626
2014-03-29
易语言正方形按钮
1
2009-05-26
观察图中各正方形图案,每条边上有n(n≥2)个点,每个图案中…
208
2011-07-16
你知道那里能买到接近正方形的 笔记本吗?
2
2011-05-03
正方形的体积
13
更多关于正方形的知识 >
等待您来回答
3回答成熟的人就不需要被珍惜吗?
7回答你觉得在大城市打拼的外来年轻人,最大的劣势是什么?
11回答月入4000、班花级别的人,为什么还单身?
5回答#有哪些情况让你感觉吃了没文化的亏?
13回答男生喜欢女汉子还是软妹子?
更多等待您来回答的问题 >
登录还没有百度账号?
立即注册
知道日报
全部文章
相关搜索
abc童装加盟费
abc英语培训学校
abc童装加盟电话
1
精彩知识在知道
快看,旮旯里有什么!
知道大数据,用数据解读生活点滴
【真相问答机】,揭穿流言!
新手帮助
如何答题
获取采纳
使用财富值
玩法介绍
知道商城
知道团队
行家认证
高质量问答
您的帐号状态正常
感谢您对我们的支持
投诉建议
意见反馈
账号申诉
智能咨询
京ICP证030173号-1 京网文【2013】0934-983号 ©2017Baidu 使用百度前必读 | 知道协议 | 百度知道品牌合作
(3,4,5,)(5,12,13)(7,24,25)勾股数组规律
规律①:至少有一个是偶数. 规律②:其中有一个数是5的整数倍 规律③:前两个数字的平方和等于最大的那个数字的平方 第一种:a=n+1,b=n-1,c^=2(n^+1) 第二种:a=n^-1,b=2n,c=n^+1 第三种:a=m^-n^,b=2mn,c=m^+n^ 第四种:a=2n+1,b=2n(n+1),c=2n(n+1)+1
八年级数学一些概念性公式(解应用题的)如:利润率=售价-进价除以进价….. 急……..求………..
1. 分式的定义:如果A、B表示两个整式,并且B中含有字母,那么式子 叫做分式。
分式有意义的条件是分母不为零,分式值为零的条件分子为零且分母不为零
2.分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。 ( )
3.分式的通分和约分:关键先是分解因式
4.分式的运算:
分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
分式除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
分式乘方法则: 分式乘方要把分子、分母分别乘方。
分式的加减法则:同分母的分式相加减,分母不变,把分子相加减。异分母的分式相加减,先通分,变为同分母分式,然后再加减
混合运算:运算顺序和以前一样。能用运算率简算的可用运算率简算。
5. 任何一个不等于零的数的零次幂等于1, 即 ;当n为正整数时, (
6.正整数指数幂运算性质也可以推广到整数指数幂.(m,n是整数)
(1)同底数的幂的乘法: ;
(2)幂的乘方: ;
(3)积的乘方: ;
(4)同底数的幂的除法: ( a≠0);
(5)商的乘方: ();(b≠0)
7. 分式方程:含分式,并且分母中含未知数的方程——分式方程。
解分式方程的过程,实质上是将方程两边同乘以一个整式(最简公分母),把分式方程转化为整式方程。
解分式方程时,方程两边同乘以最简公分母时,最简公分母有可能为0,这样就产生了增根,因此分式方程一定要验根。
解分式方程的步骤 :
(1)能化简的先化简(2)方程两边同乘以最简公分母,化为整式方程;(3)解整式方程;(4)验根.
增根应满足两个条件:一是其值应使最简公分母为0,二是其值应是去分母后所的整式方程的根。
分式方程检验方法:将整式方程的解带入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解。
列方程应用题的步骤是什么? (1)审;(2)设;(3)列;(4)解;(5)答.
应用题有几种类型;基本公式是什么?基本上有五种: (1)行程问题:基本公式:路程=速度×时间而行程问题中又分相遇问题、追及问题. (2)数字问题 在数字问题中要掌握十进制数的表示法. (3)工程问题 基本公式:工作量=工时×工效. (4)顺水逆水问题 v顺水=v静水+v水. v逆水=v静水-v水.
8.科学记数法:把一个数表示成 的形式(其中 ,n是整数)的记数方法叫做科学记数法.
用科学记数法表示绝对值大于10的n位整数时,其中10的指数是
用科学记数法表示绝对值小于1的正小数时,其中10的指数是第一个非0数字前面0的个数(包括小数点前面的一个0)
第十七章 反比例函数
1.定义:形如y= (k为常数,k≠0)的函数称为反比例函数。其他形式xy=k
2.图像:反比例函数的图像属于双曲线。反比例函数的图象既是轴对称图形又是中心对称图形。有两条对称轴:直线y=x和 y=-x。对称中心是:原点
3.性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小;
当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大。
4.|k|的几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积。
第十八章 勾股定理
1.勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2。
2.勾股定理逆定理:如果三角形三边长a,b,c满足a2+b2=c2。,那么这个三角形是直角三角形。
3.经过证明被确认正确的命题叫做定理。
我们把题设、结论正好相反的两个命题叫做互逆命题。如果把其中一个叫做原命题,那么另一个叫做它的逆命题。(例:勾股定理与勾股定理逆定理)
第十九章 四边形
平行四边形定义: 有两组对边分别平行的四边形叫做平行四边形。
平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等。平行四边形的对角线互相平分。
平行四边形的判定1.两组对边分别相等的四边形是平行四边形2.对角线互相平分的四边形是平行四边形;
3.两组对角分别相等的四边形是平行四边形; 4.一组对边平行且相等的四边形是平行四边形。
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
直角三角形斜边上的中线等于斜边的一半。
矩形的定义:有一个角是直角的平行四边形。
矩形的性质: 矩形的四个角都是直角;矩形的对角线平分且相等。AC=BD
矩形判定定理: 1.有一个角是直角的平行四边形叫做矩形。 2.对角线相等的平行四边形是矩形。
3.有三个角是直角的四边形是矩形。
菱形的定义 :邻边相等的平行四边形。
菱形的性质:菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
菱形的判定定理: 1.一组邻边相等的平行四边形是菱形。 2.对角线互相垂直的平行四边形是菱形。
3.四条边相等的四边形是菱形。S菱形=1/2×ab(a、b为两条对角线)
正方形定义:一个角是直角的菱形或邻边相等的矩形。
正方形的性质:四条边都相等,四个角都是直角。 正方形既是矩形,又是菱形。
正方形判定定理: 1.邻边相等的矩形是正方形。 2.有一个角是直角的菱形是正方形。
梯形的定义: 一组对边平行,另一组对边不平行的四边形叫做梯形。
直角梯形的定义:有一个角是直角的梯形
等腰梯形的定义:两腰相等的梯形。
等腰梯形的性质:等腰梯形同一底边上的两个角相等;等腰梯形的两条对角线相等。
等腰梯形判定定理:同一底上两个角相等的梯形是等腰梯形。
解梯形问题常用的辅助线:如图
线段的重心就是线段的中点。 平行四边形的重心是它的两条对角线的交点。 三角形的三条中线交于疑点,这一点就是三角形的重心。 宽和长的比是 (约为0.618)的矩形叫做黄金矩形。
第二十章 数据的分析
1.加权平均数:加权平均数的计算公式。 权的理解:反映了某个数据在整个数据中的重要程度。
学会权没有直接给出数量,而是以比的或百分比的形式出现及频数分布表求加权平均数的方法。
2.将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数(median);如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
3.一组数据中出现次数最多的数据就是这组数据的众数(mode)。
4.一组数据中的最大数据与最小数据的差叫做这组数据的极差(range)。
5. 方差越大,数据的波动越大;方差越小,数据的波动越小,就越稳定。
数据的收集与整理的步骤:1.收集数据 2.整理数据 3.描述数据 4.分析数据 5.撰写调查报告 6.交流
6. 平均数受极端值的影响众数不受极端值的影响,这是一个优势,中位数的计算很少不受极端值的影响。